반응형
* 본 포스팅은 나동빈 - 이코테 2021 강의 몰아보기 에서 학습한 내용을 포스팅합니다.
출처
■ 소수(Prime Number)
- 소수란 1보다 큰 자연수 중에서 1과 자기 자신을 제외한 자연수로는 나누어 떨어지지 않는 자연수이다.
- 6은 1, 2, 3, 6으로 나누어떨어지므로 소수가 아니다.
- 7은 1과 7을 제외하고는 나누어 떨어지지 않으므로 소수이다.
- 코딩 테스트에서는 어떠한 자연수가 소수인지 아닌지 판별해야 하는 문제가 자주 출제된다.
■ 소수의 판별 : 기본적인 알고리즘(Python)
# 소수 판별 함수(2이상의 자연수에 대하여)
def is_prime_number(x):
# 2부터 (x - 1)까지의 모든 수를 확인하며
for i in range(2, x):
# X가 해당 수로 나누어떨어진다면
if x % i == 0:
return False # 소수가 아님
return True # 소수임
print(is_prime_number(4))
print(is_prime_number(7))
■ 소수의 판별 : 기본적인 알고리즘 성능 분석
- 2부터 x - 1까지의 모든 자연수에 대하여 연산을 수행해야 한다.
- 모든 수를 하나씩 확인한다는 점에서 시간 복잡도는 O(X)이다.
■ 약수의 성질
- 모든 약수가 가운데 약수를 기준으로 곱셈 연산에 대해 대칭을 이루는 것을 알 수 있다.
- 예를 들어 16의 약수는 1, 2, 4, 8, 16이다.
- 이때 2 X 8 = 16은 8 X 2 = 16과 대칭이다.
- 따라서 우리는 특정한 자연수의 모든 약수를 찾을 때 가운데 약수(제곱근)까지만 확인하면 된다.
- 예를 들어 16이 2로 나누어 떨어진다는 것은 8로도 나누어 떨어진다는 것을 의미한다.
■ 소수의 판별 : 개선된 알고리즘(Python)
import math
# 소수 판별 함수(2이상의 자연수에 대하여)
def is_prime_number(x):
# 2부터 x의 제곱근까지의 모든 수를 확인하며
for i in range(2, int(math.sqrt(x)) + 1):
# x가 해당 수로 나누어떨어진다면
if x % i == 0:
return False # 소수가 아님
return True # 소수임
print(is_prime_number(4))
print(is_prime_number(7))
■ 소수의 판별 : 개선된 알고리즘 성능 분석
- 2부터 X의 제곱근(소수점 이하 무시)까지의 모든 자연수에 대하여 연산을 수행해야 한다.
- 시간 복잡도는 O(N½)이다.
■ 다수의 소수 판별
- 특정한 수의 범위 안에 존재하는 모든 소수를 찾기 위해서 에라토스테네스의 체 알고리즘을 사용한다.
■ 에라토스테네스의 체 알고리즘
- 다수의 자연수에 대하여 소수 여부를 판별할 때 사용하는 대표적인 알고리즘
- 에라토스테네스의 체는 N보다 작거나 같은 모든 소수를 찾을 때 사용
- 에라토스테네스의 체 알고리즘의 구체적인 동작 과정은 다음과 같다.
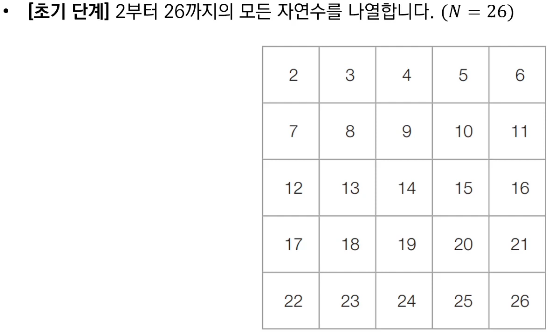
- 2부터 N까지의 모든 자연수를 나열
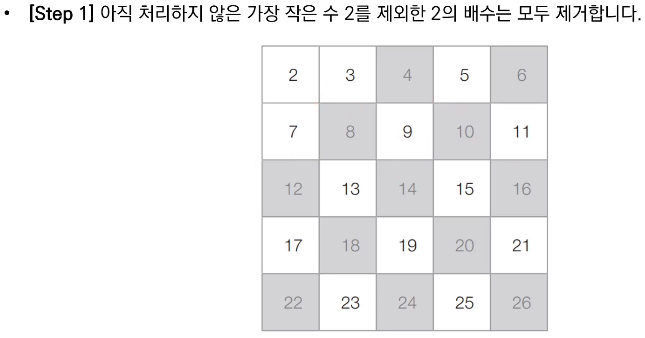
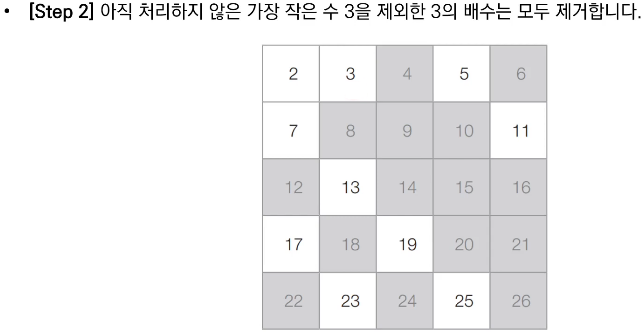
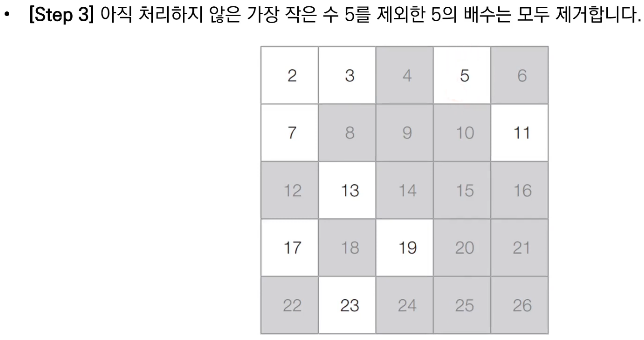
- 남은 수 중에서 아직 처리하지 않은 가장 작은 수 i를 찾는다.
- 남은 수 중에서 i의 배수를 모두 제거(i는 제거하지 않는다).
- 더 이상 반복할 수 없을 때까지 2번과 3번의 과정을 반복
■ 에라토스테네스의 체 알고리즘 동작 예시

■ 에라토스테네스의 체 알고리즘 : 구현 방법(Python)
import math
n = 1000 # 2부터 1,000까지의 모든 수에 대하여 소수 판별
array = [True for i in range(n + 1)] # 처음엔 모든 수가 소수(True)인 것으로 초기화
# 에라토스테네스의 체 알고리즘
for i in range(2, int(math.sqrt(n)) + 1): # 2부터 n의 제곱근까지의 모든 수를 확인하며
if array[i] == True: # i가 소수인 경우 (남은 수인 경우)
# i를 제외한 i의 모든 배수를 지우기
j = 2
while i * j <= n:
array[i * j] = False
j += 1
# 모든 소수 출력
for i in range(2, n + 1):
if array[i]:
print(i, end=' ')
■ 에라토스테네스의 체 알고리즘 성능 분석
- 에라토스테네스의 체 알고리즘의 시간 복잡도는 사실상 선형 시간에 가까울 정도로 매우 빠르다.
- 시간 복잡도는 O(NloglogN)이다.
- 에라토스테네스의 체 알고리즘은 다수의 소수를 찾아야 하는 문제에서 효과적으로 사용될 수 있다.
- 하지만 각 자연수에 대한 소수 여부를 저장해야 하므로 메모리가 많이 필요하다.
N이 100만이라 하더라도 밑이 2인 로그 100만은 20이고 밑이 2인 20은 4이므로 400만 정도 될 것이다.
10억을 만큼을 저장해야하는 메모리 공간이 필요하므로 비효율적일 수도 있다.
■ 투 포인터 (Two Pointers)
- 투 포인터 알고리즘은 리스트에 순차적으로 접근해야 할 때 두 개의 점의 위치를 기록하면서 처리하는 알고리즘이다.
- 흔히 2, 3, 4, 5, 6, 7번 학생을 지목해야 할 때 간단히 '2번부터 7번까지의 학생'이라고 부르곤 한다.
- 리스트에 담긴 데이터에 순차적으로 접근해야 할 때는 시작점과 끝점 2개의 점으로 접근할 데이터의 범위를 표현할 수 있다.
[문제] 특정한 합을 가지는 부분 연속 수열 찾기
- N개의 자연수로 구성된 수열이 있다.
- 합이 M인 부분 연속 수열의 개수를 구해라
- 수행 시간 제한은 O(N)이다.
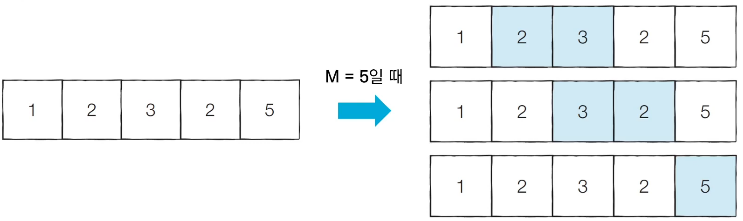
▶ 부분 연속 수열이란 하나의 수열이 있을 때 그 수열에서 연속된 일부분의 데이터만 가지는 수열을 의미한다.
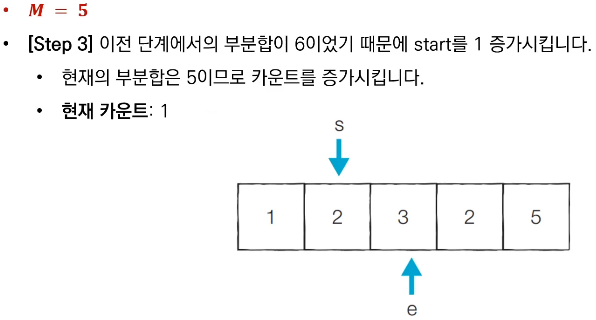
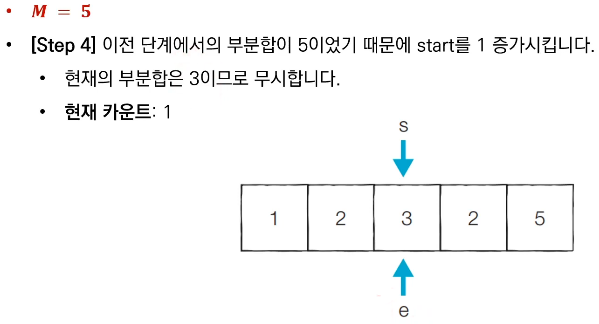
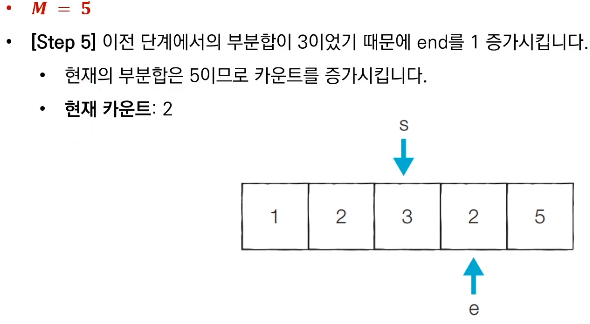
■ 문제 해결 아이디어
- 투 포인터를 활용하여 다음과 같은 알고리즘으로 문제를 해결할 수 있다.
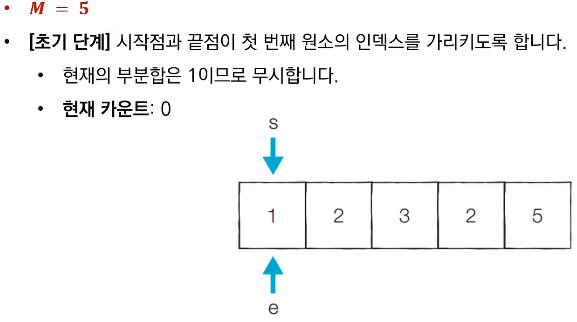
- 시작점(start)과 끝점(end)이 첫 번째 원소의 인덱스(0)를 가리키도록 한다.
- 현재 부분 합이 M과 같다면, 카운트한다.
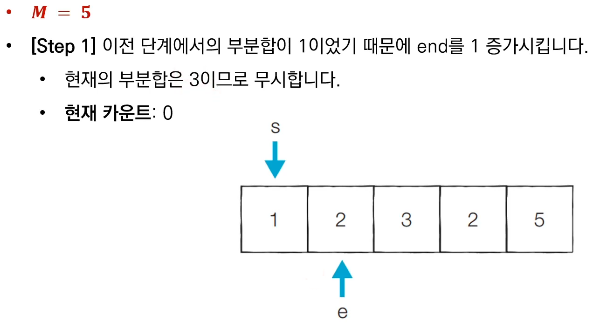
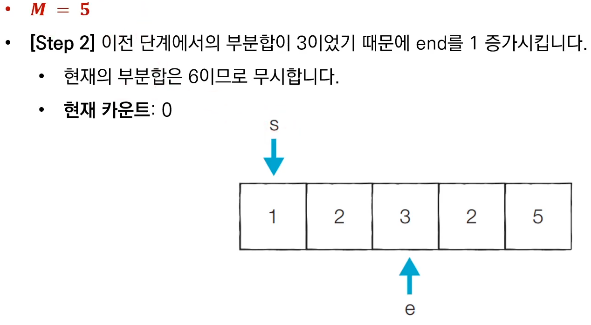
- 현재 부분 합이 M보다 작다면, end를 1증가시킨다.
- 현재 부분 합이 M보다 크거나 같다면, start를 1증가시킨다.
- 모든 경우를 확인할 때까지 2번부터 4번까지의 과정을 반복한다.



■ 답안 예시(Python)
n = 5 # 데이터의 개수 N
m = 5 # 찾고자 하는 부분합 M
data = [1, 2, 3, 2, 5] # 전체 수열
count = 0
interval_sum = 0
end = 0
# start를 차례대로 증가시키며 반복
for start in range(n):
# end를 가능한 만큼 이동시키기
while interval_sum < m and end < n:
interval_sum += data[end]
end += 1
# 부분합이 m일 때 카운트 증가
if interval_sum == m:
count += 1
interval_sum -= data[start]
print(count) # 3
[문제] 구간 합 빠르게 계산하기
- N개의 정수로 구성된 수열이 있다.
- M개의 쿼리(Query) 정보가 주어진다.
- 각 쿼리는 Left와 Right으로 구성된다.
- 각 쿼리에 대하여 [Left, Right] 구간에 포함된 데이터들의 합을 출력해야 한다.
- 수행 시간 제한은 O(N + M)이다.
■ 구간 합(Interval Sum)
- 구간 합 문제 : 연속적으로 나열된 N개의 수가 있을 때 특정 구간의 모든 수를 합한 값을 계산하는 문제
- 예를 들어 5개의 데이터로 구성된 수열 {10, 20, 30, 40 , 50}이 있다고 가정하자
- 두 번째 수부터 네 번째 수까지의 합은 20 + 30 + 40 = 90이다.
■ 문제 해결 아이디어
- 접두사 합(Prefix Sum): 배열의 맨 앞부터 특정 위치까지의 합을 미리 구해 놓은 것
- 접두사 합을 활용한 알고리즘은 다음과 같다.
- N개의 수 위치 각각에 대하여 접두사 합을 계산하여 P에 저장한다.
- 매 M개의 쿼리 정보를 확인할 때 구간 합은 P[Right] - P[Left - 1]이다.

■ 답안 예시(Python)
# 데이터의 개수 N과 전체 데이터 선언
n = 5
data = [10, 20, 30, 40, 50]
# 접두사 합(Prefix Sum) 배열 계산
sum_value = 0
prefix_sum = [0]
for i in data:
sum_value += i
prefix_sum.append(sum_value)
# 구간 합 계산 (세 번째 수부터 네 번째 수까지)
left = 3
right = 4
print(prefix_sum[right] - prefix_sum[left - 1]) # 70
반응형
'알고리즘' 카테고리의 다른 글
| 코드업 기초 100제 (0) | 2023.04.01 |
|---|---|
| [알고리즘] 그래프 이론 (신장 트리, 위상 정렬) (0) | 2023.02.22 |
| [알고리즘] 그래프 이론 (서로소 집합) (0) | 2023.02.22 |
| [알고리즘] 최단 경로 알고리즘 (2) (0) | 2023.02.17 |
| [알고리즘] 최단 경로 알고리즘 (1) (2) | 2023.02.16 |




댓글